Paper Review - [EMNLP 2014]"GloVe, Global Vectors for Word Representation" by Pennington et al., 2014
Conference : EMNLP(Empirical Methods in Natural Language Processing), 2014
1. Contributions
본 논문은 Word Analogy Task에서 SOTA를 달성한 Model을 소개했을 뿐만 아니라, 지금까지 불투명했던 성능들에 있어서 수학적인 근거를 제시했습니다. 또한, 논문에서 새로운 Model로 Global log-bilinear regression model을 제안했습니다. 당시에 Word를 Vector로 표현하면서, Semantic and Syntactic Regularities 포착하는 것에 성공했지만, Regularity의 구체적인 기원은 불투명한 상태라고 했습니다. Global log-bilinear regression model은 Global Matrix Factorization(Such as LSA)과 Local Context Window(Such as Skip-gram)의 이점들을 결합하여 Word Analogy Task에서 75%의 Accuracy로 SOTA를 달성했다고 합니다.
2. Backgrounds
LSA의 기본 아이디어는 대량의 텍스트 데이터에서 단어와 문서 사이의 관계를 분석하여, 그 과정에서 발생하는 의미적 구조를 파악하는 것입니다. 이를 통해 단어와 문서를 저차원의 의미적 공간에 매핑하게 됩니다. 구체적으로 LSA는 다음과 같은 과정을 통해 수행됩니다
- LSA의 첫 단계는 term-document 행렬을 생성하는 것입니다. 이 행렬에서 행은 개별 단어(또는 텀)를 나타내고, 열은 문서를 나타냅니다.
- 행렬의 각 요소는 해당 단어가 문서에 나타나는 빈도(Term Frequency)를 나타냅니다. 때때로 TF-IDF(Term Frequency-Inverse Document Frequency) 가중치를 적용하여 단어의 중요도를 조정하기도 합니다.
LSA는 통계적 정보를 활용하는 데에 있어서 잘 작동하나, word analogy task에서는 부진합니다. 이와 반대로 Skip-gram과 같은 방법론은 analogy task에서 성능이 좋으나, corpus의 통계적 특성을 활용하는 데에 있어서는 부진합니다.
⇒ Global Log-bilinear Regression model이 위 두 모델들의 단점을 보완하며 결합한 Model입니다.
2-2. Matrix Factorization Methods
- 행렬 분해 방법은 LSA(Latent Semantic Analysis)와 같은 초기 기법에서부터 발전해 왔으며, corpus의 통계적 정보를 포착하기 위해 큰 행렬을 낮은 순위의 근사치로 분해합니다.
- term-document 행렬: LSA에서 사용되는 term-document 행렬은 행이 단어를, 열이 문서를 나타냅니다.
- term-term 행렬: HAL(Hyperspace Analogue to Language)과 같은 기법에서는 term-term 행렬을 사용하여, 행과 열 모두 단어를 나타내고, 각 항목 값은 특정 단어가 다른 단어의 문맥 내에서 나타나는 횟수를 나타냅니다.
- 문제점: HAL과 유사한 방법의 주요 문제는 가장 빈번한 단어가 유사도 측정에 과도하게 영향을 미치는 것입니다.
- 개선책: COALS 방법에서는 co-occurence 행렬을 entropy 또는 correlation 기반으로 정규화하여 co-occurence 횟수를 더 작은 구간에 고르게 분포시키는 변환을 사용합니다.
2-3. Shallow Window-Based Methods
- 위 방법은 Local Context Window내에서 예측을 통해 단어 표현을 학습합니다. 이는 단어와 그 문맥 사이의 관계를 Modeling하는 방식입니다.
- 예시: Skip-gram과 CBOW 모델은 두 단어 벡터 간의 내적을 기반으로 한 단일 계층 아키텍처를 사용합니다.
- Skip-gram은 주어진 단어를 바탕으로 문맥을 예측합니다.
- CBOW는 주어진 문맥을 바탕으로 단어를 예측합니다.
- 성능: 이러한 모델들은 단어 유추 task에서 단어 벡터 간의 언어적 패턴을 선형 관계로 학습하는 능력을 입증했습니다.
- 단점: Shallow Window-based Method는 corpus의 co-occurence 통계에 직접 작용하지 않으며, 전체 corpus를 살펴보는 방식으로 작동하기 때문에 데이터 내의 반복되는 패턴을 충분히 활용하지 못합니다.
3. Methodology
GloVe Model은 Corpus(전체 집합)에서 단어 출현(빈도)의 통계적 특성(분포)이 Word Vector에서 어떻게 단어의 의미를 표현하는지 설명을 하고자 했습니다. 그 과정에서 GloVe Model의 Modeling에 대한 과정을 살펴봐야 합니다. 수학적인 수식들이 조금 있지만 차근차근 설명해보겠습니다.
$Let$
\(X = [X]_{ij}\) , ($X_{ij}$ 는 단어 i의 문맥에서 단어 j가 등장한 횟수를 Count한 것입니다.)
$X_{i} = \sum_{k} X_{ik}$ , ($X_{i}$는 단어 i의 전체 출현 횟수라고 볼 수 있습니다.)
$P_{ij} = P(j|i) = X_{ij} / X_{i} = X_{ij}/\sum_{j}X_{ij}$, ($P_{ij}$는 단어 i의 전체 빈도 중에서 단어 j와의 Co-occurence가 차지하는 비율(확률)이라고 볼 수 있습니다.)
이제 예시로 단어 출현의 통계적 특성이 Word Embedding에 어떻게 쓰일 수 있는지 예시로 살펴보겠습니다. 논문에서는 다음과 같은 표를 제시했습니다.
열역학적인 예시이지만, 어렵지 않습니다. $ice$와 $steam$은 온도를 의미하는 것이고 온도에 따라 $solid, gas, water$ 와 $fashion$ 중에서 적절한 상태가 있을 것입니다. 예컨대$, ice$는 $solid$와 연관이 깊을 것이고, $steam$은 $gas$와 연관이 있을 것입니다.
$k = solid$라 했을 때, $ice$와 연관이 깊고, $steam$과 연관이 낮은 것은 $P(k|ice)$ 와 $P(k|steam)$을 통해 살펴볼 수 있습니다.
\[\frac{P_{ik}}{P_{jk}} = \frac{P(k|i)}{P(k|j)} = \frac{\frac{X_{ik}}{X_{i}}}{\frac{X_{jk}}{X_j}} = \frac{\text{단어 i의 전체 빈도 중 k의 비율}}{\text{단어 j의 전체 빈도 중 k의 비율}}\]이 수식을 잘 생각해보면, $\frac{P_{ik}}{P_{jk}}$의 값이 클 수록 $i$와 $k$의 연관이 비교적 깊어지고, 값이 작을 수록 $j$와 $k$의 연관이 비교적 깊다는 것을 알 수 있습니다. 따라서 $k = solid$일 때, $P(k|ice) / P(k|steam)$의 값이 크게 나오는 것은 꽤나 직관적입니다. 나머지 예시들도 마찬가지입니다.
이제 위의 수식을 Model에서 활용하기 위해 변환해가는 과정을 확인하겠습니다. 먼저, 위의 수식을 General한 함수 $F$로 표현해줍니다. 식에 조작을 가해가면서 다음의 식을 만족하는 함수 $F$를 찾는 것이 목표입니다.
\[F(w_i, w_j, \tilde{w}_k) = \frac{P_{ik}}{P_{jk}}, \quad w, \tilde{w} \in \mathbb{R}^d\]여기서 $w$는 word vector이며, $\tilde{w}$는 context word vector입니다. Context word vector는 그 단어가 등장할 때 주변에 어떤 단어들이 함께 나타나는지의 패턴을 Modeling하는 데 사용됩니다. 여기서 vector space는 Linear property가 있어서 수식을 다음과 같이 표현할 수 있습니다.
\[F(w_i- w_j, \tilde{w}_k) = \frac{P_{ik}}{P_{jk}}, \quad w, \tilde{w} \in \mathbb{R}^d\]그러나 아직 좌변은 벡터인 반면에 우변은 스칼라라는 문제점이 있습니다. 이를 맞춰주기 위해, 좌변을 내적의 형태로 표현해줍니다.
\[F((w_i- w_j)^T \tilde{w}_k) = \frac{P_{ik}}{P_{jk}}, \quad w, \tilde{w} \in \mathbb{R}^d\]마지막으로 중요한 부분이 남았습니다. 사실 word와 context word는 서로 역할이 바뀔 수 있습니다. A문장에서는 word였던 것이 B문장에서는 context word로 쓰일 수 있고 반대도 마찬가지입니다. 이것이 수학에서는 Symmetric하다는 property로 반영이 되어야합니다. 그러나, 위의 수식은 Symmetric을 만족하지 못합니다. 따라서 Symmetric을 만족하게 만들기 위해서 $F$는 $(R,+)$와 $(R_{>0}, X)$사이에서 Homomorphism을 만족한다고 가정합니다.
- Homomorphism
와 같이 되는 함수 $F$를 Homomorphic하다고 하는데요. 쉽게 말하면, 입력으로 덧셈의 역원을 넣어 주었을 때 함수의 출력값으로는 곱셈의 역원이 나오는 성질을 말합니다. (e.g $F(a-b) = \frac{F(a)}{F(b)}$). 함수 $F$가 Homomorphic하다고 설정을 해주면, $F$는 $(R,+)$를 $(R_{>0}, X)$ mapping할 수 있는 함수가 되며, 다음과 같이 식에 조작을 가할 수 있습니다.
\[w_{i}^T \tilde{w}_k = (w_{i} - w_{j})^T \tilde{w}_k + w_{j}^T \tilde{w}_k\] \[=> F(w_{i}^T \tilde{w}_k) = F((w_{i} - w_{j})^T \tilde{w}_k + w_{j}^T \tilde{w}_k)\] \[=> F(w_{i}^T \tilde{w}_k) = F((w_{i} - w_{j})^T \tilde{w}_k )* F(w_{j}^T \tilde{w}_k) (by Homomorphism)\] \[=> F((w_i- w_j)^T \tilde{w}_k) = \frac{F(w_{i}^T \tilde{w}_{k})}{F(w_{j}^T \tilde{w}_{k})} = \frac{P_{ik}}{P_{jk}} , \quad w, \tilde{w}\in \mathbb{R}^d\]로 표현할 수 있으며, 위 과정에서 \(1) F(w_{i}^T \tilde{w}_{k}) = P_{ik}\) 임을 알았고,
\[F(w_i^T \tilde{w}_k - w_j^T \tilde{w}_k) = \frac{F(w_{i}^T \tilde{w}_{k})}{F(w_{j}^T \tilde{w}_{k})}, \quad w, \tilde{w} \in \mathbb{R}^d\]을 통해서 $2)F$는 exponential이라는 것을 알 수 있습니다. \(F(w_{i}^T\tilde{w}_k) = \exp(w_{i}^T\tilde{w}_k) = P_{ik} = \frac{X_{ik}}{X_{i}}\) 를 상기하며, $1)$ 과 $2)$를 연립하면, \(w_i^T \tilde{w}_k = \log(P_{ik}) = \log(X_{ik}) - \log(X_{i})\)라는 것을 알 수 있습니다. 마지막으로 $\log(X_{i})$는 여전히 Symmetric하지 않습니다. 논문에서는 이것을 bias term인 $b_{i}$으로 바꿔주고 $\tilde{b}_k$를 넣어줌으로, 해결하고자 했습니다.
\[w_i^T \tilde{w}_k + b_{i} + \tilde{b}_k= \log(X_{ik})\]로 표현하며 수식 유도를 마무리하게 됩니다.
그러나 우리가 처음에 설정한 행렬 $X$에서 Co-occurence가 0인 원소가 분명 있을 것입니다. 이를 해결하기 위해서 $\log(X_{ik})$를 $\log(1+X_{ik})$로 변환해주는데, 이 경우에는 빈도가 0인 원소가 1이 됨으로 무의미한 원소가 1이라는 데이터를 가지게 되어, Noise로 작용하게 됩니다. 따라서 논문에서는 최종적으로 Weighted Least Squares Regression Model을 제안합니다.
\[J = \sum_{i,j =1}^V f(X_{ij})(w_i^T \tilde{w}_k + b_{i} + \tilde{b}_k- \log(X_{ik}))^2\]where $V$ is the size of vocabulary.
Properties
- $f (0) = 0$. 만약 $f$를 연속함수로 간주한다면, $x → 0$ 일 때, 충분히 빠르게 0으로 수렴해야하며, $lim_{x→0} f (x) log2 x$ 가 유한하게 됩니다.
- $f (x)$ 는 비감소함수이고, 이 때 드물게 나타나는 co-occurrence가 과대평가되지 않게 됩니다.
- $f (x)$ 는 $x$의 큰 값에 대해 상대적으로 작게 되어, 자주 발생하는 co-occurence가 과대평가되지 않습니다.
위의 Property들을 만족하는 함수 $f$를 찾으면, $\log(X_{ik})$를 $\log(1+X_{ik})$로 변환하면서 생긴 Noise를 해소할 수 있게 됩니다. 논문에서는 함수 $f$를 다음과 같이 정의했습니다.
\[f(x) = \begin{cases} \left(\frac{x}{x_{\text{max}}}\right)^\alpha & \text{if } x < x_{\text{max}} \\1 & \text{otherwise}\end{cases}\]논문에서는 $\alpha$ = 3/4일 때, 성능이 좋다고 주장했습니다.
논문에서 제안한 모델이 Skip-gram과 같은 Window-based method과도 연관이 있다고 합니다. 이 또한 수식으로 살펴보아야 합니다. Skip-gram에서 출발해보겠습니다.
\[Q_{ij} = \frac{exp(w_{i}^T\tilde{w}_j)}{\sum_{k=1}^V exp(w_{i}^T\tilde{w}_k)}\]여기서, $Q_{ij}$는 단어 i의 문맥에서 단어 j가 등장할 확률을 Softmax형태로 표현한 것입니다. 우리가 집중해야하는 부분은 Window-based method에서는 $\log Q_{ij}$를 Maximize하는 것이 목적이라는 것입니다. 이에 근거한 목적식은 다음과 같이 표현될 수 있습니다.
\[J = -\sum_{i\in corpus, j\in context(i)} \log{Q_{ij}} = -\sum_{i=1}^V \sum_{j=1}^V X_{ij}\log Q_{ij}\]3-1에서 정의했듯이, $X_{i} = \sum_{k} X_{ik}$이고, $P_{ij} = X_{ij}/X_{i}$입니다. 이에 착안하여 식에 조작을 가하면
\[J = -\sum_{i=1}^VX_{i} \sum_{j=1}^V P_{ij}\log Q_{ij} = \sum_{i=1}^VX_{i} H(P_i, Q_i)\]와 같이 표현될 수 있습니다. $H(P_i, Q_i)$는 Cross Entropy라는 것을 생각하면 어렵지 않게 도출할 수 있습니다. 이미 위의 $J$는 앞서 제안했던 Weighted Least Squares와 유사한 형태이지만, 아쉽게도 위의 $J$는 최적화가 어려운 식입니다. 또한, 여러 바람직하지 않은 특성들도 있습니다. 예를 들어서, Cross entorpy error는 두 확률 분포 사이의 여러 measure중 하나일 뿐입니다. 또한, 상황에 따라서 성능이 나쁘게 나올 수 있습니다. 기타 등등의 이유로 다음과 같은 $J$를 제안했습니다.
\[\hat{J} = \sum_{i,j}X_i(\hat{P_{ij}} -\hat{Q_{ij}})^2\]여기서 \(\hat{P_{ij}} = X_{ij}\)이고 \(\hat{Q_{ij}} = exp(w_{i}^T\tilde{w}_j)\)는 정규화가 되지 않은 분포라고 합니다. 끝으로 $X_{ij}$가 매우 큰 값이 될 수 있으므로, 각 값에 $\log$를 취해주는 방식을 제안했습니다.
\[\hat{J} = \sum_{i,j}X_i(\log \hat{P_{ij}} - \log \hat{Q_{ij}})^2 = \sum_{i,j}X_i(w_{i}^T\tilde{w}_j - \log X_{ij})^2\]이제 이 식을 정리해주면
\[\hat J = \sum_{i,j =1}^V f(X_{ij})(w_i^T \tilde{w}_j - \log(X_{ij}))^2\]로 3-1에서와 매우 유사한 형태의 Cost function을 구할 수 있습니다.
4. Empirical Results
4-1. GloVe 모델의 성능 평가
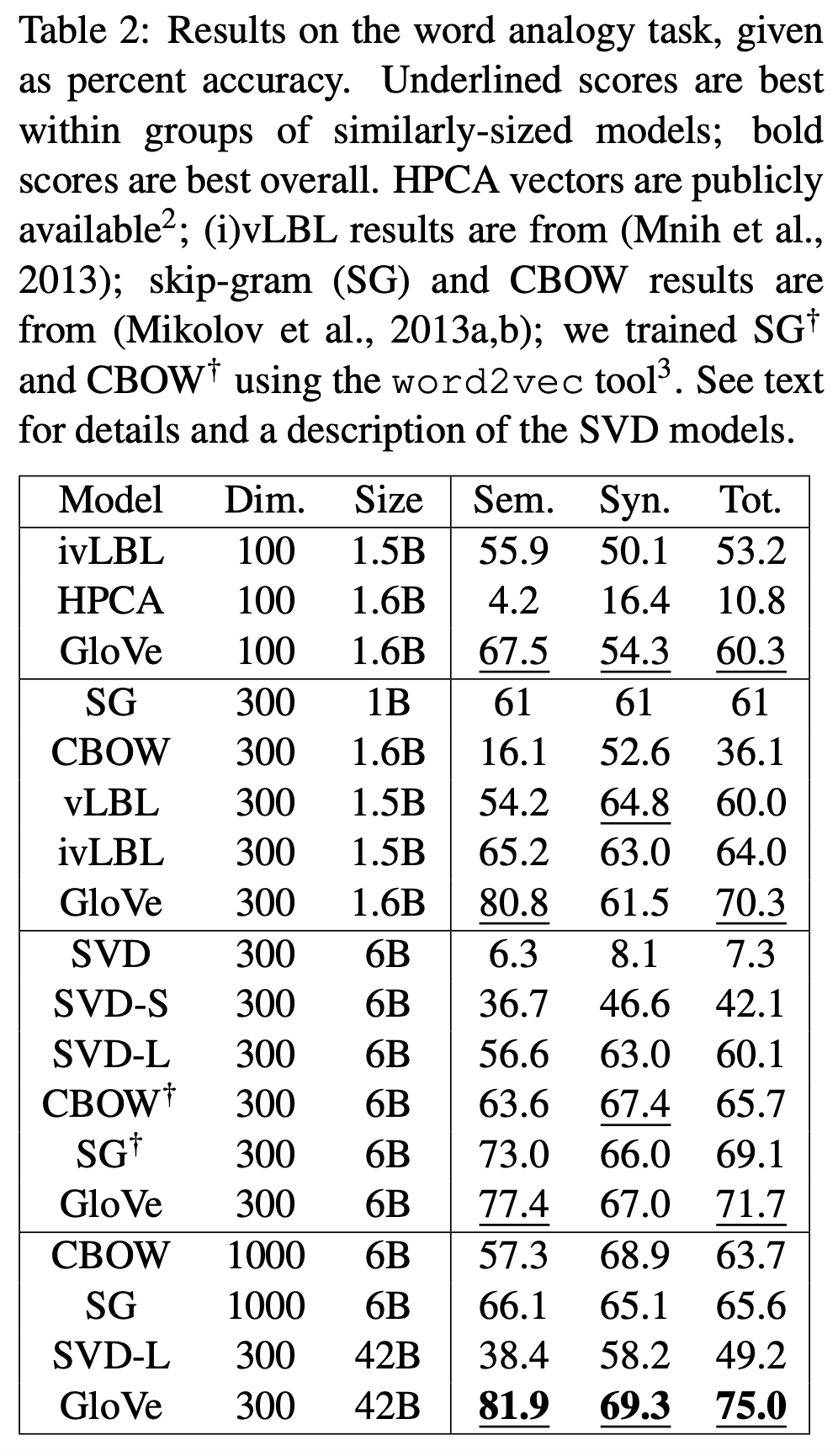
- Word Analogy Task: GloVe 모델은 단어 유추(word analogy) 태스크에서 높은 정확도를 달성하였습니다. 이는 단어 간의 의미적(semantic)과 문법적(syntactic) 관계를 벡터 공간에서 성공적으로 모델링할 수 있음을 시사합니다.
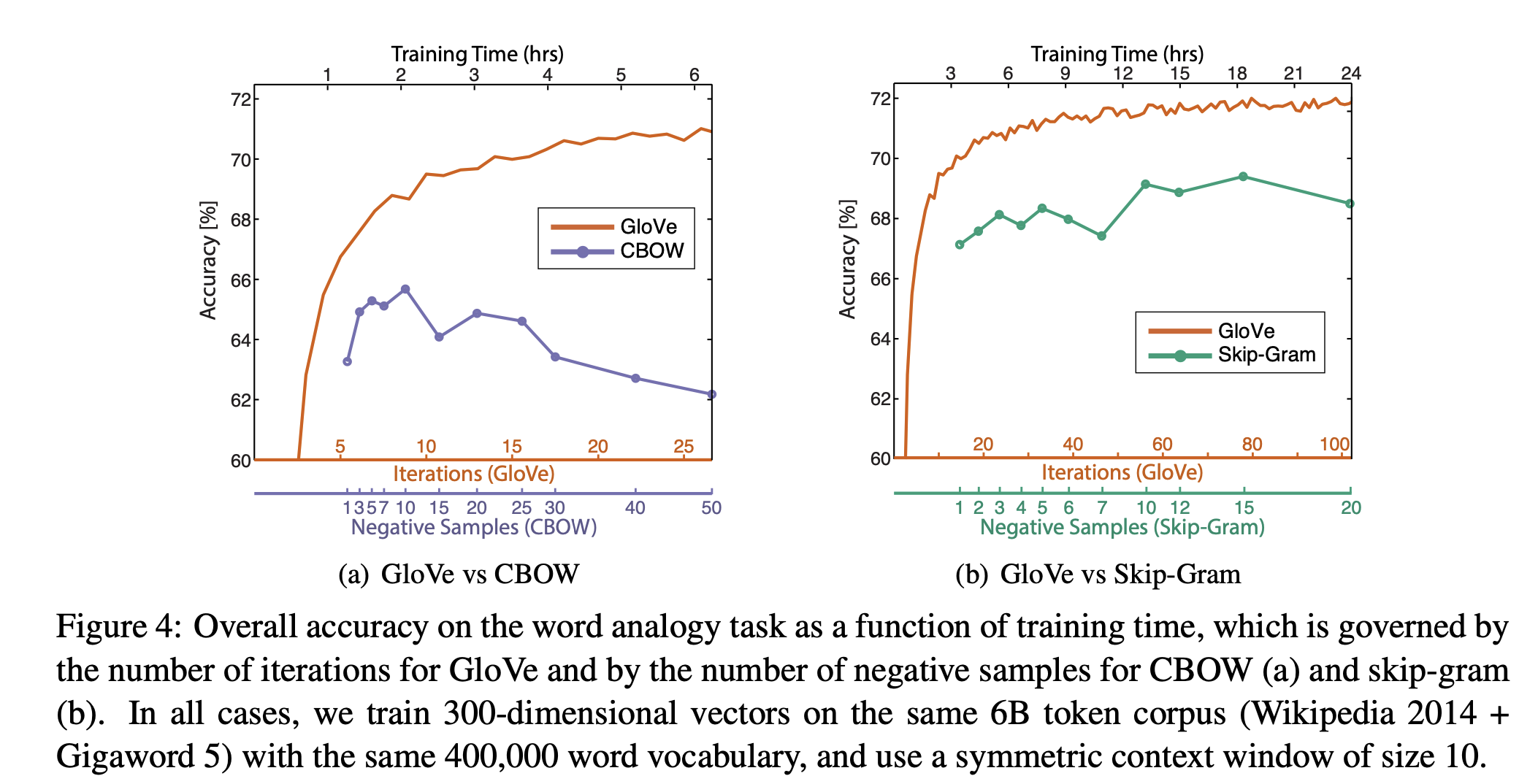
- 비교 분석: GloVe는 기존의 다른 단어 표현 방법론들, 예를 들어 Word2Vec의 Skip-gram 모델과 비교하여 상당한 성능 향상을 보였습니다. 특히, 대규모 데이터셋에서 GloVe의 우수성이 두드러졌습니다.
4-2. 주요 발견
- Vector 차원의 영향: 다양한 vector 차원(예: 100, 300, 1000차원)에서 GloVe 모델을 평가한 결과, 모델의 성능은 vector의 차원 수가 증가함에 따라 일반적으로 향상되었습니다. 그러나 특정 차원 이상에서는 성능 향상의 폭이 줄어들었습니다.
- Corpus 크기의 영향: GloVe 모델의 성능은 훈련 데이터의 크기에도 크게 의존했습니다. 더 큰 corpus에서 훈련된 모델이 더 정확한 단어 표현을 생성하는 경향을 보였습니다.
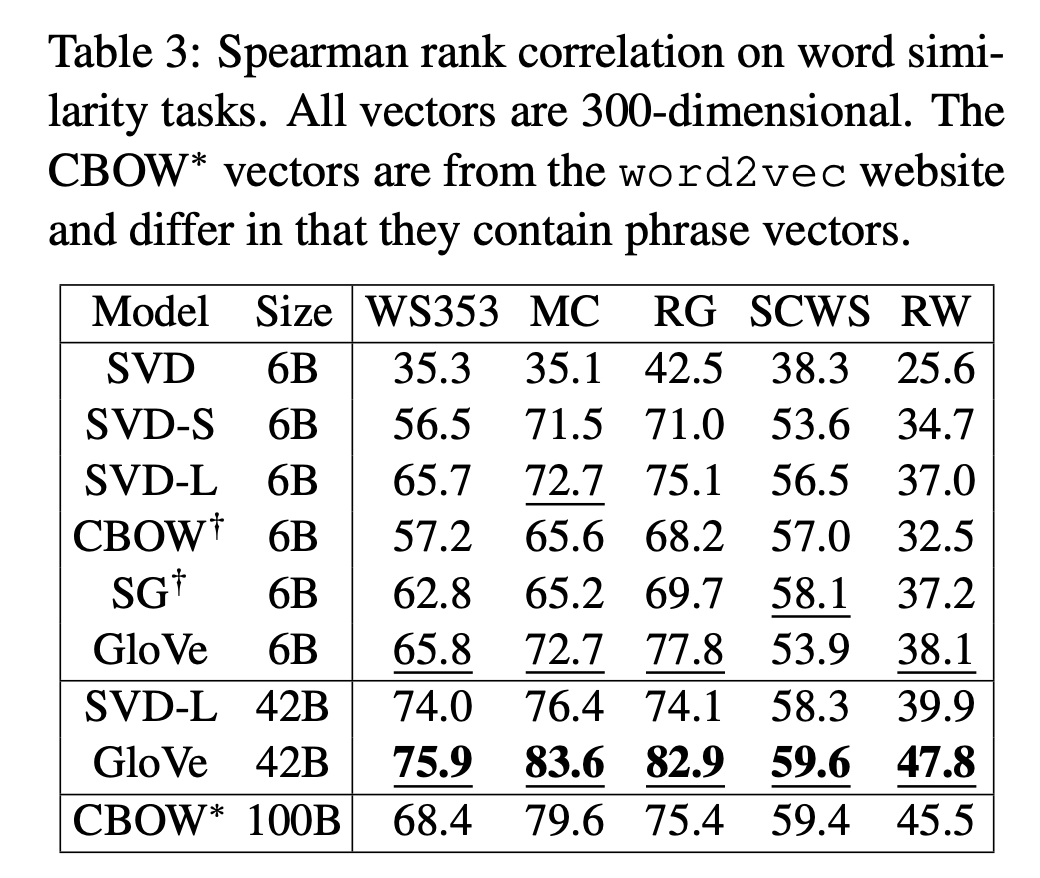
- 단어 유사성과 관계성: GloVe 모델은 단어 간의 유사성(similarity)과 관계성(analogy)을 모두 포착하는 데 효과적이었습니다. 이는 모델이 단어의 Semantic 관계뿐만 아니라, 그들 사이의 더 복잡한 패턴을 이해할 수 있음을 의미합니다.
GloVe의 결과는 이 모델이 대규모 언어 데이터에서 의미론적과 문법적 패턴을 효과적으로 포착할 수 있는 강력한 단어 표현 방법임을 보여줍니다. GloVe는 기존의 단어 Embedding 기법들과 비교하여 상당한 성능 향상을 제공했습니다.
이상으로 포스팅을 마치겠습니다.
감사합니다.